Kapitel 3 |
Ralf Wagner Leitfaden
Volkswirtschaftslehre © 1996-2002 « AM 2 | Übersicht | PDF-Druckversion | Übungsaufgaben | AM 3a» | AM 4 » |
|
| 3. Analyse
der Nachfrage (Haushaltstheorie) |
||
| Zielstellung:
Wie erklärt sich aus volkswirtschaftlicher Sicht,
wieviel (welche Menge) ein Haushalt nachfragt bzw. die
Haushalte insgesamt unter bestimmten Bedingungen
nachfragen. Ausgangsbedingung: (Ausschließlich) Haushalte sind Nachfrager nach Gütern. Sie verhalten sich rational. Ausgangspunkt der Nachfrage der Haushalte sind die Bedürfnisse der Menschen, denen man unterstellt, daß sie unendlich - d.h. unbegrenzt - sind. Welche Bedürfnisse und wieviel davon in wirkliche Nachfrage umgesetzt werden, hängt im wesentlichen von zwei Faktorbündeln ab:
Dabei kann auch auf das eigene Vermögen (W) durch das sogenannte Entsparen bzw. auf das Vermögen anderer durch einen Kredit zurückgegriffen werden. Aus Präferenzen und Einkommen entsteht beim Nachfrager für jedes Gut eine bestimmte Preisvorstellung, die auch Zahlungsbereitschaft genannt wird. Mit dieser Zahlungsbereitschaft kommt ein Verbraucher auf den Markt. Dort reagiert er auf die durch den Markt geschaffene Preissituation, d.h. er paßt sich mit seiner Mengennachfrage einem existierenden Marktpreis an (Mengenanpassung). Analysiert man das allgemeine, durchschnittliche Verbraucherverhalten, kann man es wie folgt beschreiben: Je höher der Marktpreis, desto niedriger die nachgefragte Menge - eine negative Korrelation also. Diese läßt sich grafisch darstellen. |
||
| Abb. 3-1: Idealtypisches Nachfragerverhalten | 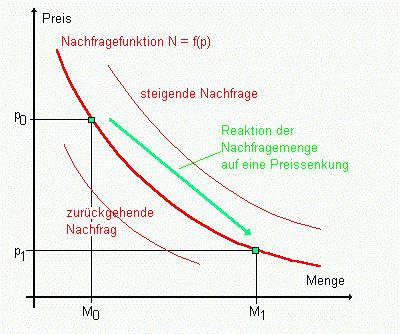 |
|
| Dieses
Nachfragerverhalten läßt sich zusätzlich dadurch erklären,
daß man den einzelnen Punkten der Nachfragefunktion je
einen individuellen Nachfrager zuweist. Das bedeutet, daß
sich alle Nachfrager in ihren Preis- und
Mengenvorstellungen unterscheiden, durch Einkommens- und
Präferenzunterschiede ergeben sich unterschiedliche
Zahlungsbereitschaften. Problem: Die Aufgabe für den Haushalt besteht nun darin, bei gegebenen Möglichkeiten (Einkommen, Vermögen, Kreditmöglichkeiten) die zu konsumierende Menge für jedes Gut (und damit für alle Güter) zu bestimmen. Als Ziel der Haushaltsnachfrage wird dabei angenommen, daß er bestrebt ist, den Nutzen (U) aus seinem Konsum zu maximieren - d.h. er versucht, bei gegebenem Einkommen (...) den größtmöglichen Nutzen zu erreichen. Das Ergebnis ist mathematisch ein Optimum und wird daher auch als Haushaltsoptimum oder (in Süddeutschland) als optimaler Einkaufspaln bezeichnet. Wie dieses zustande kommt läßt sich wie folgt erklären. Lösung a - für die Nachfrage nach einem Gut: Der deutsche Ökonom Hermmann Heinrich von Gossen (1810-1858) hat versucht, empirisch zu erklären, wie sich der Nutzen aus dem Konsum in Abhängigkeit von der konsumierten Menge verhält. Er hat dabei festgestellt, daß der Nutzenszuwachs jeweils bei der ersten konsumierten Einheit am größten ist und danach beständig abnimmt (das erste Bier schmeckt am besten usw.) bis er schließlich 0 wird und danach sogar negative Werte annimmt. |
||
| Abb. 3-2: Das erste Gossensche Gesetz (Sättigungsgesetz) | 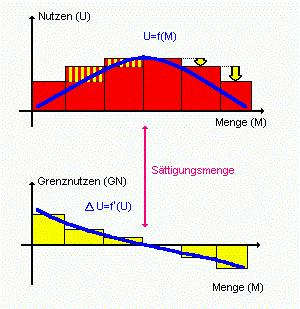 |
|
| Grenznutzen | Unterstellt
man die Richtigkeit dieser Angaben, gibt es für jeden
Verbraucher bei jedem Gut eine konsumierte Menge, wo sich
der Nutzen nicht mehr erhöht. Diese Menge nennt man Sättigungsmenge
- eine größere Menge zu konsumieren, macht keinen Sinn.
Aber auch bis zur Sättigung wird kaum ein Verbraucher
seinen Konsum treiben. Dies liegt daran, daß die Güter
ja nicht kostenfrei zur Verfügung stehen sondern einen
Preis haben. In der Tat wird der Nachfrage beim Konsum jeder weiteren Einheit den Zuwachs an Nutzen durch diesen Akt mit dem jeweiligen Preis vergleichen. Ist der
Daraus zog GOSSEN den Schluß, daß ein Haushalt solange konsumiert, bis der Nutzenszuwachs dem Marktpreis entspricht. Diesen Nutzenszuwachs beim Konsum jeweils einer Einheit mehr bezeichnete er als Grenznutzen. (sh. AM 20 Volkswirtschaftliche Schulen) |
|
| Abb. 3-3: Bestimmung der konsumierten Menge nach Gossen | 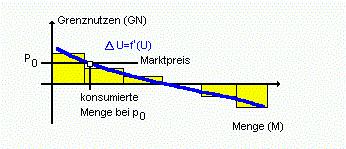 |
|
| Elastische und unelastische Nachfrage | Erhöht sich
der Marktpreis, geht die konsumierte Menge zurück und
umgekehrt. Dieses Verhalten entspricht dem in Abb. 1
gezeigten. Daher wird die Grenznutzensfunktion auch als
individuelle Nutzensfunktion eines Haushaltes in der
Nachfrage nach einem Gut bezeichnet. Allerdings gibt es auch untypisches Nachfrageverhalten, bei dem diese Preis-Mengen-Abhängigkeit nicht gilt (Snob-Effekte usw.). Auch ist es je nach Gut unterschiedlich, in welchem Umfang der Haushalt seine Nachfragemenge im Verhältnis zur verursachenden Preisänderung ist. Man bezeichnet die Nachfrage als elastisch, wenn der Haushalt in der Lage ist, z.B. auf eine Preiserhöhung mit einer noch stärkeren Mengenreduzierung zu antworten und damit den Markt wiederum zu einem niedrigeren Preis zu veranlassen. Dies ist u.a. dann möglich, wenn der Haushalt auf andere Güter ausweichen kann, die die im Preis gestiegenen zumindest teilweise im Konsum ersetzen können (sustitutive Güter - Butter und Margarine - , Gegensatz: komplementäre Güter sind Güter die sich im Verbrauch bedingen - Videorecorder und Videokassette). Bei anderen Gütern wiederum ist der Haushalt auf deren Konsum angewiesen (Arzneimittel) und er kann oder will (Benzin) bei einer Preissteigerung seine Mengennachfrage nicht oder nur wenig reduzieren. Hier reagiert er unelastisch. (Lesen Sie dazu auch AM3a: Elastizität der Nachfrage) Lösung b - für die Nachfrage nach 2 und mehreren Gütern: Da die Haushalte mehr als ein Gut konsumieren ist die o.g. Aussage diesbezüglich zu modifizieren. Das heißt zunächst einmal, daß sich ein gegebenes Einkommen auf mehrere Güter verteilt. Um das Prinzip darzustellen, geht man zunächst von 2 Gütern aus. |
|
| Abb. 3-4: Hauhaltsnachfrage nach 2 Gütern | 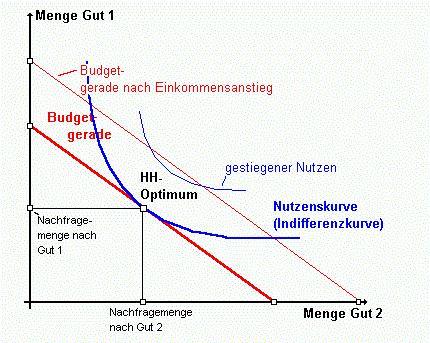 |
|
| Haushaltsoptimum Indifferenzkurve Budgetgerade |
Verteilt man
das limitierte Einkommen auf die beiden Güter 1 und 2,
so ergeben sich eine Vielzahl von Kombinationen dieser
beiden Güter, die sich mit jeweils dem gleichen
Einkommen c.p. kaufen lassen. Diese Kombinationsmöglichkeiten
werden mit der sog. Budgetgeraden dargestellt. Auf
dieser Budgetgeraden muß der Haushalt nun genau die Güterkombination
auswählen, die ihm in der Summe den größten Nutzen
stiftet. Dieses Prüfverfahren wird erleichtert, wenn man
den Nutzen aus der Güterkombination näher untersucht.
Wie in der Lehrveranstaltung gezeigt werden wird, ergibt
die Nützlichkeit solcher Güterkombinationen eine Schar
von sog. Nutzens- oder Indifferenzkurven, auf
denen der Nutzen aus der Güterkombination jeweils
konstant ist. Je weiter eine solche Kurve vom
Koordinatenursprung entfernt ist, desto größer ist das
Nutzensniveau. Der Haushalt muß also - bildlich
gesprochen - den Punkt auf der Budgetgeraden finden, der
gerade noch einen Punkt gemeinsam hat mit der am
weitesten vom Ursprung entfernten Nutzenskurve hat. Diesen Punkt bzw. diese Güterkombination bezeichnet man als Haushaltsoptimum bzw. als optimalen Einkaufsplan. Die Koordinaten dieses Punktes bestimmen gleichzeitig die nachgefragten Mengen nach den Gütern 1 und 2. Eine Veränderung von Güterpreisen, Einkommen oder der Präferenzen zu den Gütern verändern dieses Haushaltsgleichgewicht selbstverständlich. Daher ist es in den Untersuchungen erforderlich, jeweils immer nur eine Größe als Ursache zu ändern und dann die Folgen dieser Veränderung zu untersuchen. Man verdeutlicht das, indem man hinter die veränderte Größe den Zusatz c.p. setzt: ceteris paribus - unter sonst gleichen Bedingungen. Untersucht man z.B. die Veränderungen, die durch eine Einkommenserhöhung (oder Senkung) hervorgerufen werden, entstehen eine Reihe neuer Haushaltsoptima, die anzeigen, wie sich das Verbraucherverhalten bei Einkommensveränderungen entwickelt. Die Verbindung dieser Optima nennt man Einkommens-Konsum-Kurve (EKK). Legt man diese Kurve auf die einzelnen Güter um, erhält man eine Aussage über die Abhängigkeit des Güterkonsums von Einkommen (ENGEL-Kurve). Güter, deren nachgefragte Menge mit dem Einkommen der Haushalte steigt, nennt man höherwertig oder superior (z.B. elektrische Hausgeräte). Güter mit umgekehrter Reaktion nennt man vergleichsweise minderwertig oder inferior (z.B. einige Lebensmittel wie Kartoffeln). Verändert man das Haushaltsgleichgewicht nur durch die Erhöhung des Preises eines Gutes entstehen ebenfalls eine Reihe neuer Haushaltsoptima. Die Verbindung dieser Optima bezeichnet man auch als Preis-Konsum-Kurve (PKK). In der Regel wird das jetzt teurer gewordene Gut im Konsum reduziert und das im Preis gleich gebliebene mehr gekauft (Substitutionseffekt). Da sich aber bei der Preiserhöhung für ein Gut bei konstantem Einkommen insgesamt die Kaufkraft verringert (es sinkt des sog. Realeinkommen) muß der Haushalt in der Praxis mit einer bestimmten Zeitverzögerung insgesamt die Nachfrage reduzieren (Einkommenseffekt). Dadurch kann es auch beim im Preis stabil gebliebenen Gut insgesamt zu einem Nachfragerückgang kommen. Fazit: Obwohl die klassische Haushaltstheorie von einschränkenden Voraussetzungen ausgeht und von vielen aus psychologischen Faktoren absieht, erklärt sie die Phänomene der Nachfragetätigkeit der Haushalte doch zufriedenstellend und läßt eine Annahme darüber zu, welche Menge ein Haushalt unter bestimmten Bedingungen nachfragen wird. |
|
« AM 2 | Übersicht | PDF-Druckversion | Übungsaufgaben | AM 3a» | AM 4 » |