Kapitel 6 |
Ralf Wagner Leitfaden
Volkswirtschaftslehre © 1996-2002 « AM 5 | Übersicht | PDF-Druckversion | Übungsaufgaben | AM 7 » |
|
| 6.
Angebotsanalyse III: Allgemeine Unternehmenstheorie |
||
| Produktionsfunktion Kostenfunktion Ertragsgesetz |
Die im AM 5
getroffene Unterstellung, die Kosten entwickeln sich
linear mit der produzierten Menge trifft nur auf den Fall
der Massenproduktion zu. Für alle anderen Unternehmen
und für die Volkswirtschaft insgesamt müssen weitere
Untersuchungen durchgeführt werden. Dazu bedient man
sich der Unternehmensanalyse. Deren
Arbeitsschritte laufen wie folgt ab:
Diese Ableitung zeigt, daß die Abhängigkeit der Kosten von der Menge letztlich in der Produktionsfunktion begründet wird. Neben dem schon erwähnten linearen Zusammenhang bei Massenproduktion ist insbesondere die sog. ertragsgesetzliche Produktionsfunktion interessant, da sie für zahlreiche Klein- und mittelständischen Unternehmen typisch ist. Für die Darstellung einer Volkswirtschaft hat sich der sog. Cobb-Douglas-Zusammenhang durchgesetzt, der immerwährendes Wachstum mit jedoch abnehmenden Wachstumsraten beschreibt. Die Grafik zeigt eine idealtypische Entwicklung der Kosten nach dem Ertragsgesetz, während zunächst der Anstieg der Kosten immer geringer wird, nimmt er, nachdem er bei einer Menge konstant blieb, wieder ständig zu. Dies läßt sich u.a. aus der Ausnutzung einer installierten Produktionskapazität erklären. Stößt man an deren Grenzen, steigen die Kosten bei einer weiteren Erhöhung der Produktionsmenge rasch an. Erlösfunktion und BEP entsprechen den in AM 5 getroffenen Aussagen. Der Punkt B allerdings begrenzt die Expansion eines Unternehmens. |
|
| Abb. 6-1: Ertragsgesetzlicher Kostenverlauf | 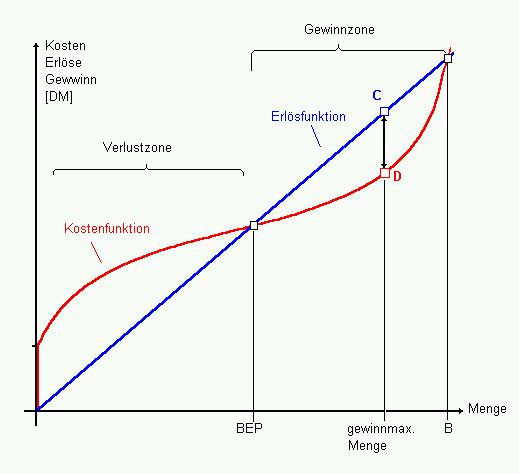 |
|
| Gewinnmaximum Grenzkosten |
Die Abbildung
1 zeigt, daß sich bei diesem Kostenverlauf das Gewinnmaximum
nicht an der Kapazitätsgrenze liegt sondern sich in
einem Gewinnintervall befindet. Innerhalb dieser Grenzen
ist genau die Menge zu bestimmen, bei der der Gewinn am
größten ist (Ziel der Unternehmertätigkeit und
notwendig zur Bestimmung der anzubietenden Menge). Es ist
sicher unmittelbar einsichtig, daß die gesuchte Menge
sich genau dort befindet, wo der Abstand zwischen Kosten
und Erlösen am größten ist (Strecke Punkt A zu Punkt B).
Vor Erreichen dieser Menge steigen die Erlöse schneller als die Kosten (Vergleich der Anstiegswinkel der entsprechenden Kurven), nach dem Gewinnmaximum ist dies genau umgekehrt. Daraus läßt sich folgern, daß sich das Gewinnmaximum genau dort befindet, wo der Anstieg der Kosten gleich dem Anstieg der Erlöse ist. Das läßt sich noch weiter vereinfachen, wenn man bedenkt, daß der Erlösanstieg von einer verkauften Mengeneinheit zur nächsten je genau dem Marktpreis für ein Stück entspricht - oder der Anstieg der Erlöskurve ist gleich dem Marktpreis. Der Anstieg der Kostenkurve entspricht dem Zuwachs der Kosten bei der Herstellung jeweils einer Mengeneinheit mehr. Diese Größe wird als Grenzkosten (GK) bezeichnet und ist, wie Abb. 1 zeigt, veränderlich. Mathematisch betrachtet handelt es sich bei den Grenzkosten um die erste Ableitung der Kostenfunktion, beim Preis um die Grenzerlöse und somit die erste Ableitung der Erlösfunktion. Das Gewinnmaximum befindet sich daher bei der Menge, wo die Grenzkosten gleich dem Marktpreis sind, bzw. GK = P. Diese Menge wird durch das Unternehmen angeboten. Wie im AM 5 gezeigt, bewirken natürlich auch bei ertragsgesetzlichen Kostenverläufen Veränderungen von Kostenbestandteilen, vom Marktpreis und der Kapazität eine Veränderung des BEP und hier auch des Gewinnmaximums. Dies soll in der Abb. 2 gezeigt werden, in der jeweils die ersten Ableitungen der Graphen von Abb. 1 dargestellt sind, also Grenzkosten und Grenzerlöse (Preis). Wie zu ersehen ist, wird ein Unternehmen bei Preiserhöhungen mit einer steigenden Angebotsmenge reagieren und umgekehrt. Die "Bestimmungslinie" ist dabei die Grenzkostenfunktion. Sie wird daher auch als individuelle Angebotsfunktion bezeichnet. Die Entscheidungsfreiheit der Unternehmen besteht jedoch nicht entlang der gesamten Grenzkostenfunktion, wie nachfolgend gezeigt werden soll. |
|
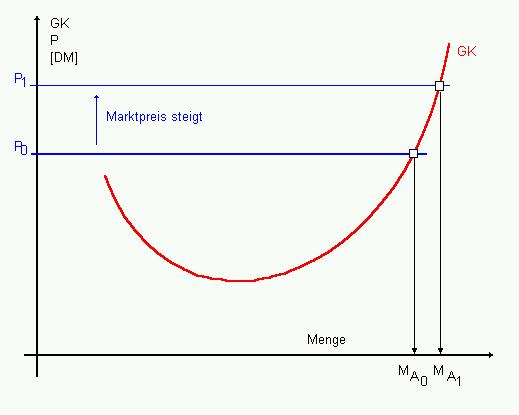
| Abb.6-2:
Grenzkosten und Preis |
 |
|
| Betriebsoptimum Betriebsminimum Deckungsbeitrag Isokostengerade Isoquante |
Es ist sicher
nachvollziehbar, daß der Anbieter eine Verringerung des
Marktpreises nicht ständig folgen kann. Er muß den
Marktpreis nicht nur mit den Grenzkosten vergleichen
sondern auch mit den Kosten, zu denen er in der Lage ist,
eine bestimmte Menge anzubieten, den Stückkosten. Liegt
der Marktpreis über den Stückkosten, kommt ein Angebot
zustande. Sind beide gleich groß, so arbeitet der
Unternehmer kostendeckend und wird also auch am Markt
bleiben. Da die Kosten gedeckt und gleichzeitig der Preis
für den Nachfrager niedrig ist, wird dieser Zustand (GK
= P = Stückkosten) auch als volkswirtschaftliches
Betriebsoptimum bezeichnet. Geht der Preis weiter zurück,
wird der Unternehmer auch noch am Markt bleiben, solange
er Löhne und Lieferanten bezahlen kann, also seine
variablen Kosten deckt. Das, was er über die variablen
Kosten erhält, wird als Deckungsbeitrag (... für
seine fixen Kosten) bezeichnet. Sinkt der Preis jedoch
unter die variablen Stückkosten, ist ein Angebot sinnlos.
Das Unternehmen verschwindet vom Markt, da es von diesem
als unwirtschaftlich "eingestuft" wurde. Der
Zustand, wo der Unternehmer gerade noch seine variablen
Kosten deckt, wird Betriebsminimum genannt und
kann nur kurzfristig "durchgehalten" werden.
Nachtrag /Exkurs: Betrachtet man die Möglichkeiten, die ein Unternehmen hat jedoch noch näher, muß man feststellen, daß die beiden wesentlichen Produktionsfaktoren Arbeit und Kapital sich in bestimmten Relationen gegenseitig ersetzen können. D.h., sie müssen auch in der Angebotsanalyse getrennt und variabel berücksichtigt werden. Geht man von 2 Produktionsfaktoren aus, die ein Unternehmer mit einer bestimmten Geldmenge kaufen kann, ergibt sich eine Vielzahl von Kombinationsmöglichkeiten dieser beiden Faktoren, welche jeweils gleiche Kosten verursachen. In der grafischen Darstellung wird dies daher auch als Isokostengerade bezeichnet. Unten den vielen Kombinationsmöglichkeiten der Isokostengerade muß der Unternehmer nun genau die wählen, die ihm den größten möglichen Output und damit Erlös erbringt. Es läßt sich zeigen, daß in dem Arbeit-Kapital-Diagramm eine Schar von Kurven entsteht, die jeweils einen konstanten Output abbilden und die daher auch Isoquanten genannt werden. Je weiter die Isoquanten vom Koordinatenursprung entfernt sind, desto höher ist der Output; er wächst von Isoquante zu Isoquante in gleichen absoluten Beträgen. |
|
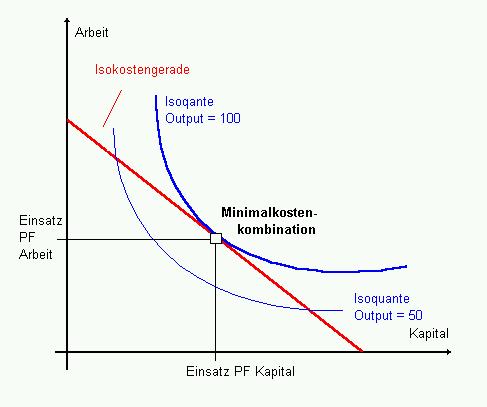
| Abb.
6-3: Minimalkosten- kombination |
 |
|
| Minimalkosten- kombination Expansionspfad economy of scale |
Man kann
sehen, das sich die optimale Kombination von Arbeit und
Kapital dort befindet, wo die Isokostengerade gerade noch
einen Punkt gemeinsam mit der am weitesten vom Ursprung
entferntesten und gerade noch erreichbaren Isoquante hat.
Diesen Punkt nennt man Minimalkostenkombination.
Die Verbindung von Minimalkostenkombinationen, die während
der Ausweitung eines Unternehmens (oder einer
Volkswirtschaft) entstehen, wird als Expansionspfad
bezeichnet. Der Punkt der Minimalkostenkombination ändert sich, wenn sich z.B. die Kosten für einen Produktionsfaktor ändern. Ein Ersatz durch den anderen wird dann angezeigt. Auch läßt sich ableiten, daß die Minimalkostenkombination dann erreicht ist, wenn das Verhältnis der Grenzproduktivitäten der beiden Produktionsfaktoren zu ihren jeweiligen Faktorkosten gleich ist. Dies wiederum bedeutet, daß die Löhne nur im Maße des Wachstums der Arbeitsproduktivität steigen können, allerdings auch der Zins gemessen an der Kapitalproduktivität. Werden die Abstände zwischen den Isoquanten immer größer, heißt das, das ein gleicher Produktionssprung mit wachsenden Aufwänden erkauft wird. Solch ein Unternehmen ist kostenprogressiv und zum Scheitern verurteilt. Umgekehrt deuten geringer werdende Abstände auf Kostendegression und wachsende Effizienz. Man spricht auch von economy of scale. |
|
« AM 5 | Übersicht | PDF-Druckversion | Übungsaufgaben | AM 7 » |